TUGAS STATISTIKA BAB 2 CARA PENYAJIAN DATA

RANGKUMAN STATISTIKA

BAB 2 “CARA PENYAJIAN DATA”

1.    Penyajian Data dalam Bentuk Tabel Frekuensi.

Data dapat kita sajikan dalam bentuk tabel atau daftar. Jika data yang akan disajikan cukup besar maka harus dikelompokan terlebih dahulu, kemudian di susun dalam bentuk tabel yang disebut daftar sebaran frekuensi atau daftar distribusi frekuensi.

a.   Daftar Distribusi Frekuensi.

·           Daftar Distribusi Frekuensi Data Tunggal.

Contoh : Hasil nilai ulangan bahasa indonesia dari 30 siswa :

·            Daftar Distribusi Frekuensi Data Kelompok.

Data yang di kelompokkan dalam kelas-kelas dengan interval yang sama, maka daftar distribusi frekuensi data berkelompok contohnya sebagai berikut :

 

Beberapa istilah yang penting dalam membuat daftar distribusi frekuensi data berkelompok antara lain sebagai berikut :

a)      Kelas interval.

Pada data di atas terdapat 5 kelas, yaitu :

Kelas interval 9 – 12, meliputi nilai 9, 10, 11, 12

Kelas interval 13 – 16

Kelas interval 17 – 20

Kelas interval 21 – 24

Kelas interval 25 – 28

b)      Batas kelas.

Pada setiap kelas, nilai terkecil d sebut batas bawah kelas dan nilai terbesar di sebut batas atas kelas. Sebagai contoh, pada kelas interval 9 – 12, 9 merupakan batas bawah kelas dan 12 sebagai batas atas kelas.

c)       Tepi kelas.

Tepi kelas adalah setengah dari jumlah batas atas dan batas bawah dua kelas interval yang berurutan. Sebagai contoh, kelas pertama 9 – 12 dan kelas kedua 13 – 16, maka tepi kelas adalah ½ (12 + 13) = 12,5 yang merupakan tepi atas (t_a) kelas pertama dan juga merupakan tepi bawah (t_b) kelas kedua.

d)      Panjang kelas.

Panjang kelas di sebut juga lebar kelas atau interval kelas, yaitu selisih antara tepi atas dan tepi bawah dari tiap interval yang sama. Sebagai contoh, data yang di sajikan pada daftar distribusi frekuensi di atas, mempunyai panjang kelas 4.

e)      Titik tengah kelas.

Nilai titik tengah kelas adalah setengah dari jumlah batas bawah kelas dan batas atas kelas. Sebagai contoh, kelas interval 9 – 12 mempunyai titk tengah ½ (9 + 12) =10,5. Selisih tiap titik tengah kelas yang berurutan sama dengan panjang kelas.

·           Cara menyusun Daftar Distribusi Frekuensi Berkelompok.

Beberapa langkah yang perlu di perhatikan dalam menyusun daftar distribusi frekuensi berkelompok adalah sebagai berikut :

a)    Menentukan nilai data terbesar, X_maks, dan nilai terkecil , X_min , kemudian di      tentukan jangkauannya (J) dengan rumus :

J = X­_maks – X_min

b)   Menentukan banyaknya kelas interval. Salah satu cara untuk menentukan banyaknya kelas interval (k) dari n buah data adalah berdasarkan aturan Sturgess, yaitu :

K = 1 + 3,3 log n

Pada umumnya di ambil nilai 5 ≤ k ≤ 15, tetapi bila jangkauannya besar di ambil

Nilai k : 10 ≤ k ≤20.

c)    Menentukan panjang kelas (c) dengan rumus :

c = J/k

d)   Menyusun daftar distribusi frekuensi dengan menetapkan kelas-kelas sehingga nilai statistik minimum termuat dalam kelas interval terendah, tetapi tidak harus sebagai batas bawah kelas. Selanjutnya, menetapkan frekuensi tiap kelas yang dapat di lakukan dengan menggunakan rumus.

b.  Daftar Distribusi frekuensi Kumulatif, Frekuensi Relatif, dan Frekuensi Kumulatif relatif.

Daftar Distribusi frekuensi kumulatif dapat di susun dari daftar distribusi frekuensi berkelompok. Terdapat dua jenis frekuensi kumulatif, yaitu kumulatif kurang dari tepi atas (f_k ≤ t_a) dan frekuensi kumulatif lebih dari tepi bawah (f_k ≥ t_b).

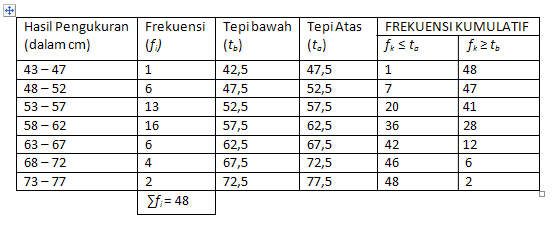
Contoh : Daftar distribusi frekuensi kumulatif, misal :

 

Setiap frekuensi f_i, dalam daftar distribusi frekuensi yang dinyatakan dalam persentase di sebut frekuensi relatif (f_r). frekuesi relative dapat di tentukan dengan rumus :

f_r = f_i /n X 100%

Selanjutnya daftar distribusi frekuensi kumulatif relatif dapat di susun dari daftar distribusi kumulatif. Seperti halnya frekuensi kumulatif, terdapat dua jenis frekuensi kumulatif relatif, yaitu frekuensi kumulatif relatif kurang dari tepi atas (f_kr  ≤ t_a) dan frekuensi kumulatif relatif lebih dari tepi bawah (f_kr ≥ t_b ). Kedua frekuensi kumulatif relative tersebut dapat di tentukan dengan rumus:

(f_kr ≤ t_a ) =(f_k ≤ t_a )/n X 100%                 (f_kr ≥ t_b ) =(f_k ≥ t_b )/n X 100%

2.        Penyajian Data dalam Bentuk Diagram (Garis, Batang, Lingkaran, Pictogram, Histrogram, dan Polygon).

     a.      Diagram Garis.

Adalah grafik berupa garis, diperoleh dari beberapa ruas garis yang menghubungkan titik-titik pada bidang bilangan. Pada grafik garis digunakan dua garis yang saling berpotongan. Pada garis horizontal (sumbu-X) ditempatkan bilangan-bilangan yang sifatnya tetap, seperti tahun dan ukuran-ukuran.
Pada garis tegak (sumbu-Y) ditempatkan bilangan-bilangan yang sifatnya berubah-ubah.

Contohnya  tentang perkembangan volume jumlah kendaraan yang melintasi jalan A dalam kurun waktu pukul 0.00 s/d 19.12

Gambar: Diagram garis.

b.      Diagram Batang.

      Adalah grafik data berbentuk persegi panjang yang lebarnya sama dan dilengkapi dengan skala atau ukuran sesuai dengan data yang bersangkutan. Setiap batang tidak boleh saling menempel atau melekat antara satu dengan lainnya dan jarak antara setiap batang yang berdekatan harus sama. 

Ada berbagai bentuk, yaitu: Grafik batangan tunggal (single bar chart), Yaitu grafik yang terdiri dari satu batangan untuk menggambarkan perkembangan (trend) dari suatu karakteristik. Grafik batangan berganda (multiple bar chart), Yaitu grafik yang terdiri dari beberapa garis untuk menggambarkan beberapa hal/kejadian sekaligus.

 

Gambar: Diagram Batang.

c.      Diagram Lingkaran. 

Yaitu grafik yang menggambarkan perbandingan nilai-nilai dari suatu karakteristik. Untuk mengetahui perbandingan suatu data terhadap keseluruhan, suatu data lebih tepat disajikan dalam bentuk diagram lingkaran. Grafik data berupa lingkaran yang telah dibagi menjadi juring-juring sesuai dengan data tersebut. Bagian-bagian dari keseluruhan data tersebut dinyatakan dalam persen atau derajat.

Gambar: Diagram Lingkaran.

d.      Diagram Pictogram. 

Pictogram adalah bentuk penyajian data statistika dalam bentuk gambar-gambar. Gambar yang digunakan disesuaikan dengan objek yang dideskripsikan yang digunakan untuk mewakili sejumlah objek.  

 

Gambar: Diagram Pictogram.

e.      Diagram Histogram. 

Penyajian distribusi frekuensi menggunkan gambar yang berbentuk diagram batang tegak. Antara dua bantang yang berdampingan tidak terdapat jarak lebar batang merupakan lebar interval di mulai dari tepi bawah sampai tepi atas interval. 

Tepi Bawah    = Batas Bawah – 0.5 

Tepi Atas        = Batas Atas + 0.5

Gambar: Diagram Histogram.

f.      Diagram Polygon. 

Apabila pada titik-titik tengah dari histogram dihubungkan dengan garis dan batang-batangnya dihapus, maka akan diperoleh poligon frekuensi. Berdasarkan contoh di atas dapat dibuat poligon frekuensinya seperti gambar berikut ini.

   

Gambar : Diagram Polygon.